Phân biệt góc đồng vị, góc so le trong và góc cùng phía

Tổng quan các góc tạo bởi một đường thẳng cắt hai đường thẳng

Trong hình học, khi một đường thẳng cắt hai đường thẳng khác, điểm giao nhau sẽ tạo ra các góc tại từng vị trí giao cắt. Đường thẳng cắt này thường được gọi là đường cắt hoặc đường thẳng thứ ba. Hai đường thẳng bị cắt có thể là song song hoặc không song song nhưng trong chương trình Toán lớp 7, trường hợp thường gặp nhất là hai đường thẳng song song.

Tại mỗi điểm giao nhau giữa đường cắt và hai đường thẳng, ta thu được 4 góc. Như vậy, khi một đường thẳng cắt hai đường thẳng, tổng cộng sẽ tạo ra 8 góc. Những góc này có mối quan hệ đặc biệt với nhau và được phân thành nhiều loại khác nhau.

Cách nhận biết các cặp góc đặc biệt

Dưới đây là các góc đặc biệt thường gặp trong những bài tập toán lớp 7.

Góc so le trong

Định nghĩa:
Hai góc được gọi là góc so le trong khi chúng nằm ở hai phía đối nhau của đường cắt, đồng thời đều nằm giữa hai đường thẳng bị cắt.

Cách nhận biết:

- Cùng nằm giữa hai đường thẳng.

- Nằm về hai phía đối nhau của đường cắt.

- Không kề nhau, không nằm trên cùng một đường thẳng.

Ví dụ: Nếu đường thẳng a cắt hai đường b và c tại A và B, thì hai góc $\hat{1}$ và $\hat{2}$ nằm đối nhau qua đường cắt và cùng trong khoảng giữa hai đường b, c sẽ là một cặp góc so le trong.

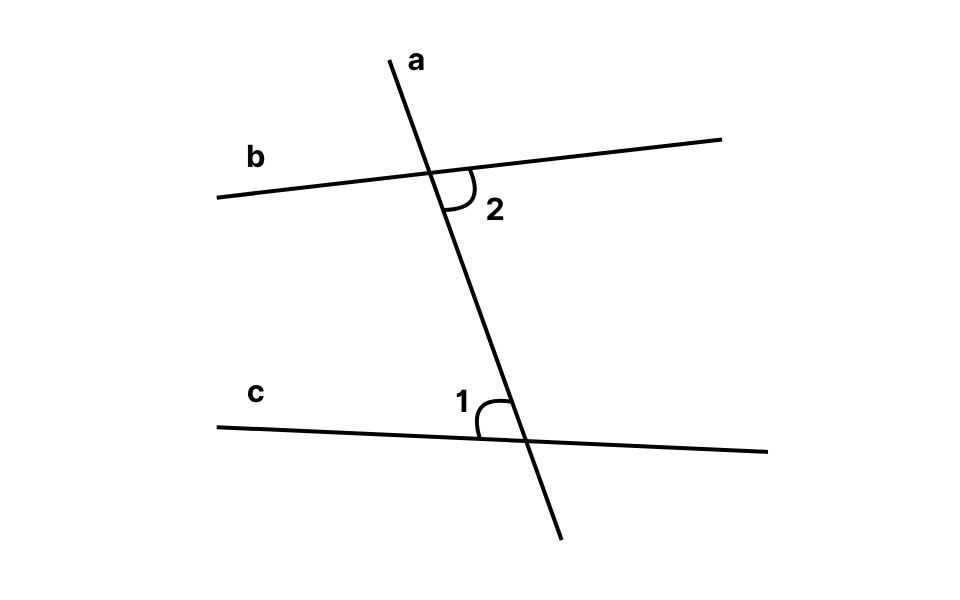
Góc so le ngoài

Định nghĩa:
Hai góc được gọi là góc so le ngoài nếu chúng nằm ở hai phía đối nhau của đường cắt, và nằm ở phía ngoài hai đường thẳng bị cắt.

Cách nhận biết:

- Nằm ở phía ngoài hai đường thẳng bị cắt.

- Nằm về hai phía đối nhau của đường cắt.

- Không kề nhau.

Ví dụ: Trên hình vẽ có đường thẳng d cắt hai đường m và n, các góc nằm ngoài khoảng giữa hai đường m, n và nằm lệch nhau qua đường d sẽ là một cặp góc so le ngoài.

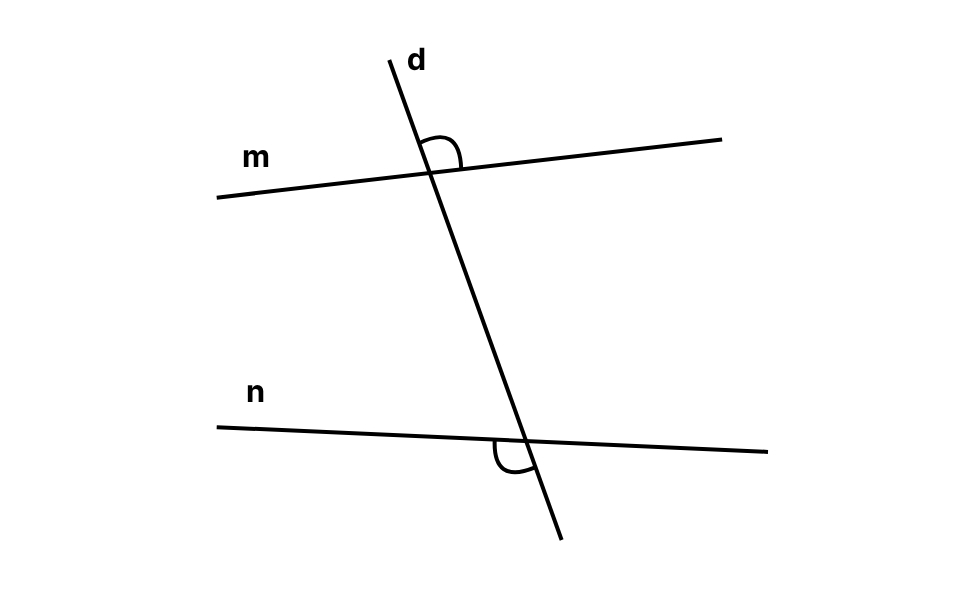
Góc đồng vị

Định nghĩa:
Hai góc được gọi là góc đồng vị khi chúng nằm cùng phía với nhau so với đường cắt và ở cùng vị trí tương ứng trên hai đường thẳng bị cắt.

Cách nhận biết:

- Cùng phía so với đường cắt.

- Nằm ở vị trí tương ứng trên hai đường thẳng.

- Có cùng hướng mở.

Ví dụ: Nếu hai góc đều ở phía trên bên phải tại hai điểm cắt của đường thẳng t với hai đường a và b, thì đó là một cặp góc đồng vị.

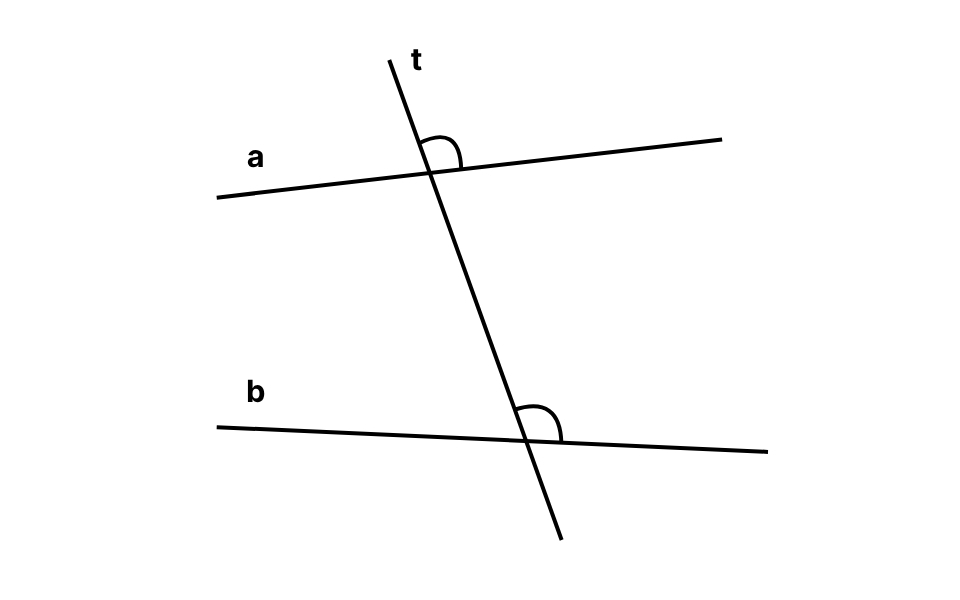
Góc trong cùng phía

Định nghĩa:
Hai góc được gọi là góc trong cùng phía nếu chúng nằm cùng phía với nhau của đường cắt và cùng nằm giữa hai đường thẳng bị cắt.

Cách nhận biết:

- Cùng nằm giữa hai đường thẳng.

- Nằm cùng phía so với đường cắt.

- Không nằm trên cùng một đường thẳng.

Ví dụ: Nếu hai góc nằm trong khoảng giữa hai đường thẳng x và y và cùng nằm bên trái hoặc bên phải đường cắt d thì đó là một cặp góc trong cùng phía.

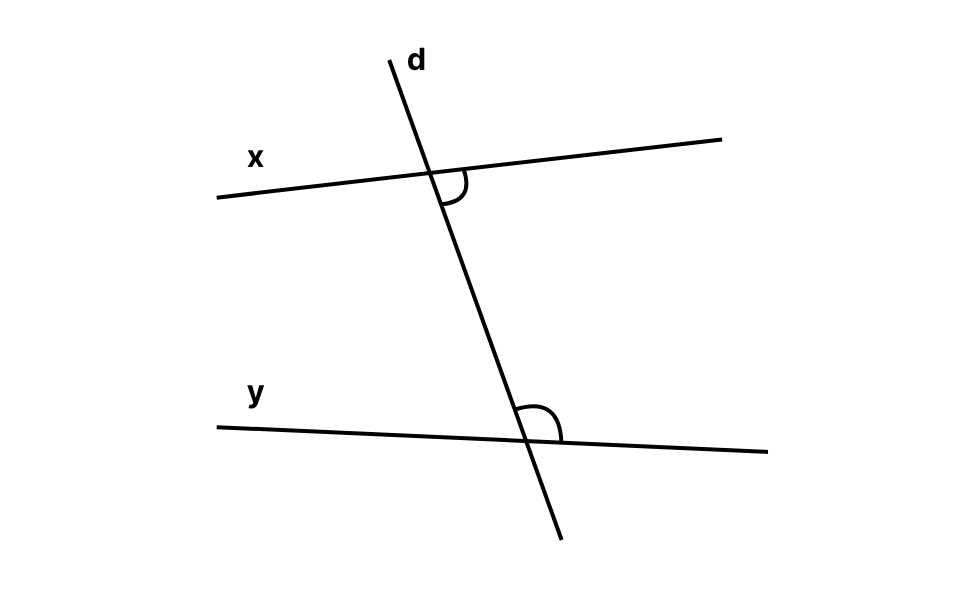
Mối liên hệ giữa các cặp góc và hai đường thẳng song song

Khi một đường thẳng cắt hai đường thẳng khác, các cặp góc đặc biệt được hình thành không chỉ giúp phân biệt vị trí mà còn phản ánh mối quan hệ giữa hai đường thẳng đó. Đặc biệt, nếu hai đường thẳng bị cắt là song song, các cặp góc sẽ thỏa mãn những tính chất cụ thể. Dưới đây là những nội dung cơ bản cần nắm vững.

Hai đường thẳng song song tạo ra những cặp góc bằng nhau

Khi hai đường thẳng bị cắt là song song, các cặp góc sau sẽ có số đo bằng nhau:

Góc so le trong: Là hai góc nằm ở hai bên đường cắt và nằm giữa hai đường thẳng. Nếu hai đường thẳng là song song thì các cặp góc so le trong có số đo bằng nhau.

Góc so le ngoài: Là hai góc nằm ở hai bên đường cắt và nằm ngoài hai đường thẳng. Nếu hai đường thẳng là song song thì các góc so le ngoài cũng bằng nhau.

Góc đồng vị: Là hai góc nằm cùng phía của đường cắt và ở cùng vị trí tương ứng đối với hai đường thẳng. Với hai đường thẳng song song, các cặp góc đồng vị sẽ bằng nhau.

Tính chất bổ sung của góc trong cùng phía

Bên cạnh các cặp góc bằng nhau, góc trong cùng phía cũng mang tính chất riêng khi hai đường thẳng là song song:

- Hai góc trong cùng phía là hai góc nằm cùng phía của đường cắt và nằm giữa hai đường thẳng.

- Nếu hai đường thẳng là song song, tổng số đo của hai góc trong cùng phía bằng 180 độ.

Bài tập về góc đồng vị, góc so le trong, góc cùng phía

Dưới đây là các dạng bài tập về góc đồng vị, góc so le trong, góc cùng phía giúp bạn rèn luyện hiệu quả và củng cố vững chắc kiến thức đã học nhé.

Dạng cơ bản

Bài 1. Cho hai đường thẳng a và b bị cắt bởi đường thẳng c, tạo thành hai góc so le trong có số đo lần lượt là $75^\circ$ và $x^\circ$. Hỏi giá trị của x bằng bao nhiêu để a//b?

Lời giải:
Khi hai đường thẳng bị cắt bởi một đường thẳng thứ ba tạo thành hai góc so le trong bằng nhau, thì hai đường thẳng đó song song.
=> Để a//b, ta cần:
$x = 75^\circ$

Đáp án: $x = 75^\circ$

Bài 2. Hai đường thẳng song song bị cắt bởi đường thẳng c, tạo thành một góc so le ngoài có số đo là $120^\circ$. Hãy tính số đo góc so le ngoài còn lại.

Lời giải:
Trong hai đường thẳng song song, góc so le ngoài bằng nhau.
=> Góc còn lại cũng bằng $120^\circ$

Đáp án: $120^\circ$

Bài 3. Cho hai đường thẳng song song bị cắt bởi đường thẳng thứ ba, tạo ra một góc đồng vị có số đo là $65^\circ$. Hãy xác định số đo góc đồng vị còn lại.

Lời giải:
Hai góc đồng vị bằng nhau khi hai đường thẳng song song.
=> Góc còn lại cũng bằng $65^\circ$

Đáp án: $65^\circ$

Bài 4. Đường thẳng c cắt hai đường thẳng a và b, tạo thành hai góc trong cùng phía có số đo lần lượt là $110^\circ$ và $70^\circ$. Hỏi hai đường thẳng a và b có song song không?

Lời giải:
Hai góc trong cùng phía bù nhau (tổng $= 180^\circ$) => hai đường thẳng song song
$110^\circ + 70^\circ = 180^\circ$=> Thỏa mãn điều kiện

Đáp án: Có, a//b

Dạng nâng cao

Bài 5. Cho hình vẽ có hai đường thẳng a và b bị cắt bởi đường thẳng c. Biết góc tạo thành tại giao điểm giữa a và c là $110^\circ$, và góc đồng vị với góc đó tại giao điểm giữa b và c là x. Tính x và xác định điều kiện để a//b.

Lời giải:
Góc đồng vị bằng nhau khi a//b.
=> Để a//b: $x = 110^\circ$

Đáp án:

$x = 110^\circ$

Khi $x = 110^\circ$ thì a//b

Bài 6. Đường thẳng d cắt hai đường thẳng m và n. Tại giao điểm với m, góc so le trong là $65^\circ$, còn tại giao điểm với n, góc so le ngoài là x. Biết rằng m//n. Tính x.

Lời giải:

m//n => các cặp góc so le trong và so le ngoài bằng nhau nếu cùng phía.
=> $x = 65^\circ$

Đáp án: $x = 65^\circ$

Bài 7. Đường thẳng a cắt hai đường thẳng b và c. Biết tại giao điểm với b, có góc trong cùng phía với giao điểm tại c là $75^\circ$, còn góc so le trong tại giao điểm với c là $105^\circ$. Hỏi hai đường thẳng b và c có song song không?

Lời giải:

Xét hai góc trong cùng phía: $75^\circ + 105^\circ = 180^\circ$=> thỏa mãn điều kiện bù nhau
→ b//c

Đáp án: Có, b//c

Nắm vững kiến thức về góc đồng vị, góc so le trong và góc cùng phía sẽ giúp học tốt hơn và rèn luyện khả năng tư duy logic và phân tích hình học. Hệ thống giáo dục online Học là Giỏi hy vọng rằng bài viết đã giúp bạn nắm chắc kiến thức và hiểu rõ hơn về cách nhận biết hai đường thẳng vuông góc.